Métricas de Desempenho em Modelos de IA (parte 2)

Por: Dr. Arnaldo de Carvalho Junior

1. INTRODUÇÃO

Este post continua a tratar métricas de desempenho iniciadas no post anterior [1], onde foram abordadas as métricas de desempenho de modelos de IA para classificação.

Neste post serão abordadas as métricas de desempenho de regressão, utilizadas em modelos de IA para
aproximação de funções, identificação de sistemas, predições, entre outras aplicações [2].

Primeiro, segue uma introdução da Regressão Linear/Múltipla Linear.

1.1. Regressão Linear / Múltipla

A Regressão é uma técnica cujo objetivo é predizer o valor de uma variável dependente (Y) quando se tem um conjunto de valores que são as variáveis independentes (X). A Regressão Linear é uma das técnicas mais básicas em aprendizado de máquinas (machine learning – ML) que se pode utilizar para realizar previsões [3][4]. 

Uma Equação de Regressão é dada em (1), onde ‘E’ significa o erro que é introduzido quando o modelo realmente não se encaixa nos dados. O objetivo de um bom modelo de regressão é minimizar esse erro.

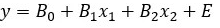
O erro é dado pela diferença entre o valor real (y) e o valor predito (ŷ) pelo modelo.

2. MÉTRICAS DE REGRESSÃO

Usadas quando a variável alvo é contínua [5]. Exemplo: preços de casas, previsão de temperatura, valores de estoque, etc. A seguir são apresentadas métricas utilizadas para avaliar modelos de regressão:

a) Raiz do erro quadrático médio (root mean square error – RMSE): Mede a raiz quadrada das diferenças quadráticas médias entre os valores previstos e reais. Penaliza fortemente grandes erros, tornando-o ideal para modelos onde grandes desvios são críticos.

b) Erro quadrado (square error – SE): A diferença quadrada bruta entre os valores previstos e reais. Útil para enfatizar erros atípicos.

c) Erro Absoluto Médio (mean absolute error – MAE): Mede as diferenças absolutas médias entre os valores previstos e reais. Mais fácil de interpretar e menos sensível a outliers em comparação com RMSE.

Essas métricas ajudam a quantificar o desempenho do sistema e orientam a melhoria contínua durante o desenvolvimento e implantação do modelo de IA [5].

A seguir são apresentadas métricas utilizadas para avaliar modelos de regressão, tais como MAE, MAPE, MSE, RMSE, R^² e R^² ajustado.

2.1 MAE

O erro médio absoluto (MAE) pode ser calculado conforme a Equação (2). Nesta equação há o calculo da média da diferença entre o valor predito ŷ e o real y. Quanto menor o valor de MAE, significa que melhor são os resultados preditos pelo modelo de ML [6][7].

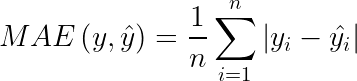
O valor de saída da equação tem a mesma escala dos dados utilizados para previsão, tornando mais fácil a sua interpretação. Se o valor de MAE resultante for igual a 10,05 m, por exemplo, este resultado significa que o modelo pode estar errando em média 10,05 m para mais quanto para menos (erro de
±10,05 m) em relação ao valor correto. Por esta razão que este resultado precisa ser levado em consideração para a tomada de decisão quando analisando previsão futura [6]. Mas o quanto este erro representa em relação ao valor real percentualmente?

2.2. MAPE

O erro percentual absoluto médio (mean absolute percentual error – MAPE) é uma métrica que mostra a porcentagem de erro em relação aos valores reais. A Equação (3) apresenta o cálculo de MAPE que é semelhante ao MAE, mas com o acréscimo de uma divisão por |y|. Então se o resultado do MAPE for igual a 35% significa que o modelo de IA faz previsões que em média a diferença entre o valor previsto e o real equivale a ±35% do valor real [6].

Ao observar a Equação (3) nota-se que caso o valor de y seja 0, ocorrerá um erro, devido a divisão por zero. Por isso que a biblioteca scikit-learn utiliza a tratativa de colocar um número muito pequeno, representado por ε, cujo valor é 2,220446049250313e-16. A métrica MAPE é uma das métricas mais usadas para reportar a performance do modelo de IA, oferecendo uma compreensão mais abrangente do resultado do MAE.

2.3. MSE

O erro quadrático médio (mean square error – MSE) nada mais é do que a média dos quadrados da diferença entre os valores observados e previstos. Ele é dado pela Equação (4).

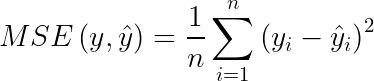
Onde n é o número de termos, y_i significa o valor observado para o i-ésimo termo e ŷ_i refere-se ap valor previsto para esse termo específico. A diferença é o termo Erro. Soma-se os quadrados de todos os termos de erro e divide-se pelo grau de liberdade (número de variáveis independentes, ou n).
Mas por que ao quadrado? Para que o erro seja acumulado em vez de erros negativos cancelarem erros positivos.

A métrica MSE apresenta um problema de interpretabilidade. Por haver a elevação ao quadrado, a unidade fica distorcida, em outras palavras, se a unidade medida for metros (m), o resultado será em m². Por isso que uma adaptação da MSE é a RMSE que será apresentada a seguir.

2.4. RMSE
RMSE é a raiz do MSE, conforme a Equação (5). O RMSE é basicamente o mesmo cálculo de MSE, contendo ainda a mesma ideia de penalização entre diferenças grandes do valor previsto e o real. No entanto, para lidar com o problema da diferença entre unidades, é aplicada a raiz quadrática. Assim a unidade fica na mesma escala que o dado original, sendo o resultado da métrica melhor interpretável [6].

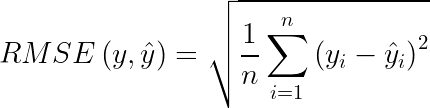
Nesta equação há o cálculo da diferença entre o valor y e ŷ, contudo com a elevação do resultado ao quadrado. Mas para deixar o resultado na mesma escala que os dados, é aplicado a raiz quadrada no resultado. Apesar de o valor ter a mesma unidade, ele não costuma se assemelhar ao resultado encontrado de MAE, demonstrando como os outliers podem estar impactando nas previsões do modelo. Mas a sua interpretabilidade pode seguir a mesma lógica, onde o resultado da métrica sendo igual a 70,0 m, significa que o modelo pode estar errando em ±70,0 m. Por essa razão, esta métrica pode ser uma boa opção quando é preciso ter uma avaliação mais criteriosa sobre as previsões do modelo.

2.5. R^²
O R-quadrado, R-dois ou coeficiente de determinação, é uma medida estatística de quão próximos os dados estão da linha de regressão ajustada. Ele também é conhecido como o coeficiente de determinação ou o coeficiente de determinação múltipla para a regressão múltipla. A definição do R^² é bastante simples: é a porcentagem da variação da variável resposta que é explicada por um modelo linear [7]. Ou:

R^² = Variação explicada/Variação total (Equação (6))

Os valores de y são os valores verdadeiros e o ӯ é a média desses valores, enquanto que ŷ são os valores preditos. Os resultados de R^² ficam entre 0 e 1, quanto mais perto de 1 melhor e pior para resultados perto de 0. O R^² está sempre entre 0 e 100%:

• 0% indica que o modelo não explica nada da variabilidade dos dados de resposta ao redor de sua média.
• 100% indica que o modelo explica toda a variabilidade dos dados de resposta ao redor de sua média.

Em geral, quanto maior o R^², melhor o modelo se ajusta aos seus dados. No entanto, existem condições importantes para esta diretriz.

A proporção de variância na variável dependente que é prevista a partir das variáveis independentes. O valor varia de 0 a 1.

1 mostra que a regressão explica perfeitamente a relação. 0 o oposto.

Se A proporção de variância na variável dependente que é prevista a partir das variáveis independentes. O valor varia de 0 a 1. 1 mostra que a regressão explica perfeitamente a relação. 0 o oposto.
Se R^² (Leia como R-Squared)= 0,45 para a equação (1) de regressão do item 1.2, então significa que 45% da variabilidade em sim é explicado pelas variáveis x₁ e x₂.

No entanto há uma falha. À medida que o número de termos aumenta, o R^² pode permanecer constante ou aumentar. Isso acontece mesmo que não haja uma boa relação entre as variáveis e a variável dependente [5]. Assim sendo, utilizando somente a métrica R^², será que um valor de 0,5 já seria o suficiente para colocar o modelo em produção? Faz-se necessário aproximar ainda mais o seu resultado para 1? Para responder a essas questões, recomenda-se sempre utilizar outras métricas para uma análise mais completa sobre a performance do modelo de IA [7].

Depois de elevá-lo ao quadrado, é necessário reduzir a escala para as unidades originais.

2.6. R^² Ajustado

R² Ajustado é um refinamento sofisticado da métrica R² convencional, sendo uma ferramenta poderosa no escopo da avaliação de modelos. À medida que novos preditores são introduzidos, o R² Ajustado adapta-se dinamicamente, ascendente ou descendente, com base na medida em que estes preditores melhoram o desempenho do modelo. Este ajuste perspicaz transcende as limitações do R² convencional, que captura apenas a proporção de variância explicada pela variável independente(s). Um valor ajustado que considerará a relação entre as variáveis. Diminuirá o valor para variáveis que não melhoram o modelo existente. A fórmula para o R² ajustado é dada pela Equação (7) [8].

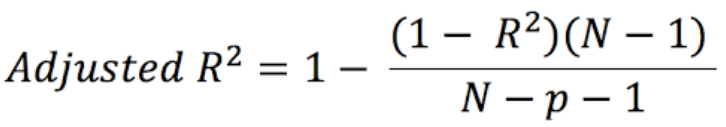
Em total contraste com o R² convencional, que permanece indiferente ao número de preditores utilizados, o R² ajustado aparece como um avaliador perspicaz e sensato, penalizando profundamente a inclusão de características irrelevantes ou redundantes que não têm impacto significativo na previsão da variável alvo. Esta métrica astuta considera cuidadosamente a contagem de variáveis independentes implementadas no processo de previsão, abrindo caminho para uma avaliação mais abrangente e equitativa das proezas preditivas do modelo.

Ao ajustar seu valor com base no número de preditores, o R² ajustado eleva o processo de avaliação do modelo para um escalão superior, orientar os pesquisadores para a seleção dos preditores mais influentes e pertinentes, ao mesmo tempo que desencoraja a incorporação de variáveis supérfluas. Este ajuste refinado equipa os cientistas de dados com uma ferramenta poderosa e informada, mantendo a curadoria de modelos mais parcimoniosos que atingem um equilíbrio ideal entre precisão preditiva e parcimônia.

De tudo isso, deve ter tido agora alguma ideia sobre como os modelos podem ser comparados em uma regressão.

3. RESUMO

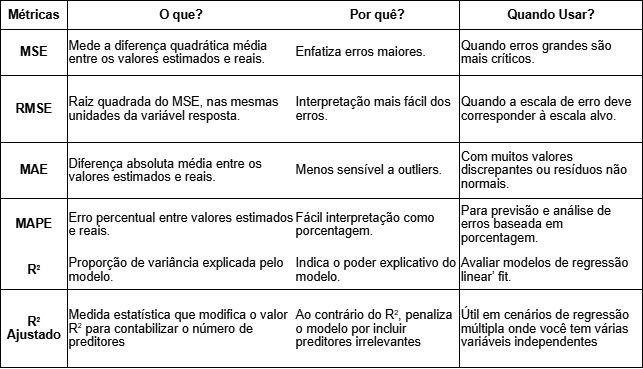
Com base no apresentado até aqui a Tabela 1 a seguir aponta as principais diferenças entre as métricas de avaliação de regressão MSE, RMSE, MAE, MAPE, R² e R² ajustado [9].

4. CONCLUSÃO

Neste post foram apresentadas algumas das métricas mais utilizadas para avaliar o modelos de regressão acompanhado de suas particularidades.

Como visto a métrica a ser adotada depende da solução que o modelo pode vir a resolver com o modelo de ML. Uma abordagem comum, fácil de ser implementada e muito interessante é utilizar todas para se ter diferentes perspectivas em relação a performance do modelo.

Dentre as métricas apresentadas, o R² é uma métrica muito comum, mas difícil de ser utilizada sozinha para se tirar conclusões completas sobre a performance do modelo. O R² ajustado é um resultado muito importante para saber se o conjunto de dados é adequado ou não. Alguém faz uma equação de regressão para validar se o que pensa sobre a relação entre duas variáveis é também validado pela equação de regressão. Quanto maior for o R² ajustado, melhor é a equação de regressão, uma vez que implica que a variável independente escolhida para determinar a variável dependente seja corretamente escolhida. Idealmente, um investigador procurará o coeficiente de determinação mais próximo dos 100%.

Tanto MAE e MAPE apresentam uma boa interpretabilidade, principalmente para relatório dos resultados do modelo. Já as métricas MSE e RMSE são afetadas por valores discrepantes, o que pode ser importante quando é preciso ter uma avaliação mais criteriosa do modelo de ML.

5. REFERÊNCIAS
[1] CARVALHO JUNIOR, A. Métricas de Desempenho em Modelos de IA (parte 1), EAILAB, IFSP, 2025. Disponível em: <https://eailab.labmax.org/2025/05/06/metricas-de-desempenho-em-modelos-de-ia-parte-1/>. Acessado em Mai 10, 2025.

[2] CARVALHO, A., JUSTO, J.F., ANGÉLICO B.A. et al. Model reference control by recurrent neural network built with paraconsistent neurons for trajectory tracking of a rotary inverted pendulum, Applied Soft Computing, 2022, 109927, ISSN 1568-4946, DOI: 10.1016/j.asoc.2022.109927.

[3] KAKANADAN, U. Regression and performance metrics — Accuracy, precision, RMSE and what not!, Medium, 2024. Disponível em: <https://medium.com/analytics-vidhya/regression-and-performance-metrics-accuracy-precision-rmse-and-what-not-223348cfcafe>. Acessado em Jul 31, 2024.

[4] AMORIM, N. Regressão Linear Simples com Python e sklearn, Dev 4.0, 2021. Disponível em: <https://dev4lab.github.io/posts/regressao-lienar-com-python/#:~:text=Regressão%20Linear%20%C3%A9%20uma%20das%20t%C3%A9cnicas>. Acesso em Mai 12, 2025.

[5] DILMEGANI, C. How To Measure AI Performance, AI Multiple Research, 2025. Disponível em: <https://research.aimultiple.com/how-to-measure-ai-performance/>. Acessado em Mai 05, 2025.

[6] MINITAB, Análise de regressão: Como interpretar o R-quadrado e avaliar a qualidade de ajuste?, Blog do Editor, Minitab, 2019. Disponível em: <https://blog.minitab.com/pt/analise-de-regressao-como-interpretar-o-r-quadrado-e-avaliar-a-qualidade-de-ajuste>. Acessado em Mai 06, 2025.

[7] OLIVEIRA JUNIOR, C. Métricas para Regressão: Entendendo as métricas R², MAE, MAPE, MSE e RMSE, Medium, 2021. Disponível em:<https://medium.com/data-hackers/prevendo-números-entendendo-métricas-de-regressão-35545e011e70>. Acesso em Mai 12, 2025.

[8] RAJESH, P. S. What is Adjusted R-Squared, Net-Informations.com, 2024. Disponível em: <https://net-informations.com/ds/psa/adjusted.htm>. Acesso em Mai 13, 2025.

[9] KUMAR, A. MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to use?, Analytics Iogue, 2024. Disponível em: <https://vitalflux.com/mse-vs-rmse-vs-mae-vs-mape-vs-r-squared-when-to-use/>. Acesso em Mai 13, 2025.