Função de Ativação, o Núcleo da Composição de Neurônios Artificiais
- INTRODUÇÃO
As redes neurais artificiais – RNAs (artificial neural networks – ANN) são algoritmos poderosos, muito utilizados em aplicações de inteligência artificial (IA) e aprendizado de máquina (machine learning – ML).
As RNAs são capazes de “aprender” uma determinada função ou reconhecimento de padrões, despertando interesse em diversas áreas do conhecimento humano, de medicina diagnóstica a robótica, automação e controle de sistemas complexos [1].
As RNAs são constituídas de neurônios artificiais cujas funções matemáticas são inspiradas em neurônios biológicos, constituindo a base de redes neurais artificiais. A Figura 1 apresenta um exemplo de interligação de neurônios para compor uma RNA.
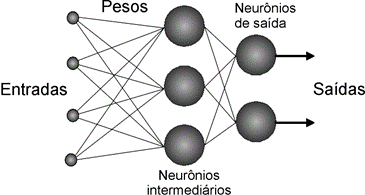
Fonte: Adaptado de [2]
Apesar de não ter a mesma complexidade de um cérebro, as RNAs apresentam duas similaridades básicas com as redes neurais biológicas [3]:
a. possibilidade de descrição de seus blocos de construção por dispositivos computacionais simples;
b. as conexões entre os neurônios determinam a função da rede.
A Figura 2 apresenta uma representação de um neurônio biológico. Já a Figura 3 apresenta um neurônio artificial de múltiplas entradas.
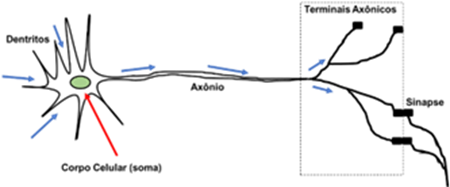
Fonte: Adaptado de [1]
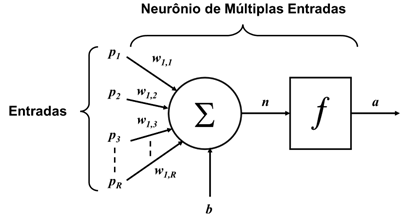
Fonte: Adaptado de [1]
No neurônio biológico, os dentritos são filamentos responsáveis por receber os sinais de informações para as células. O corpo celular, ou soma, reúne as informações recebidas pelos dentritos. Já o axônio transporta os impulsos elétricos que partem do corpo celular até as diversas ramificações com dilatações bulbosas conhecidas como terminais axônicos (ou terminais nervosos), que estabelecem as conexões sinápticas com outras células [1].
Conforme a Figura 3, o neurônio artificial consiste de 2 etapas. A primeira é a somatória ponderada dos sinais de entrada, que em seguida são aplicados a uma função de ativação. Os pesos (w) representam a força das sinapses e são multiplicados aos valores das respectivas entradas e somados, juntamente com um valor de ajuste ou bias (b). O resultado desta soma (n) é então aplicado a uma função de ativação (f) e apresentado na saída (a) do neurônio artificial. Um neurônio artificial pode ser descrito como:
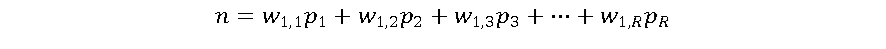
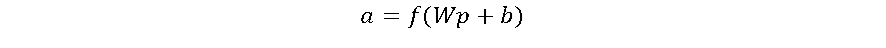
As funções de ativação são um elemento fundamental das RNAs. Elas essencialmente decidem se um neurônio deve ser ativado ou não. Em outras palavras, se o que o neurônio está recebendo é relevante para a informação fornecida ou deve ser desprezada [4].
Várias funções f podem ser utilizadas, mas é importante que a função de ativação adotada seja derivável, de modo a permitir a elaboração de algoritmos de regressão para calibração, ou “aprendizado”, dos pesos e bias do neurônio [3]. Pode ser demonstrado que se a função de ativação for não linear, uma RNA de duas camadas pode ser um aproximador universal de função [5].
2. FUNÇÕES DE ATIVAÇÃO
As Figuras 4 e 5 apresentam algumas das funções de ativação mais utilizadas em projetos de RNAs [6].
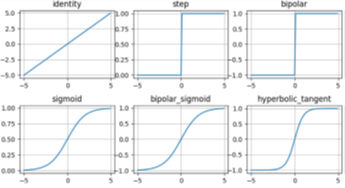
Fonte: Adaptado de [6]

Fonte: Adaptado de [6]
2.1. Função Step
A função de ativação mais elementar é a Função Degrau (Step), onde o classificador é baseado em um limiar de ativação (threshold). Ela foi utilizada nos primeiros neurônios artificiais foi introduzido em 1943 por W. McCulloch e W. Pitts [3].
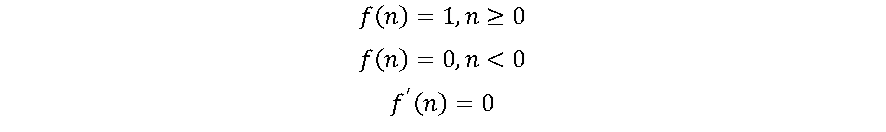
A função Step é mais teórica do que prática, pois em geral há mais de uma classe de dados para serem classificados. Além disso, o gradiente da função Step é zero, dificultando processos de aprendizagem da RNA.
2.2. Função Linear ou Identidade
A função identidade também é uma função simples, cuja derivada resulta em uma constante (α), não importa o valor da entrada x. Isso dificulta os processos de aprendizagem da RNA. Todavia a função linear pode ser ideal para tarefas simples, onde a interpretabilidade é altamente desejada [4], como por exemplo o neurônio da camada de saída da RNA.
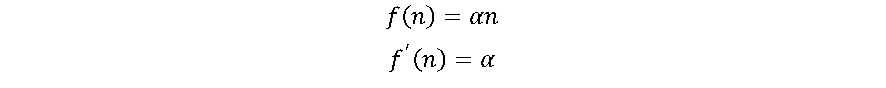
2.3. Função Sigmoide
Uma das funções de ativação mais utilizadas nas RNAs é a log-sigmoide, por ser não linear e pela facilidade de implementação de sua derivada no processo ajuste dos pesos, conforme as equações a seguir [1],[6].
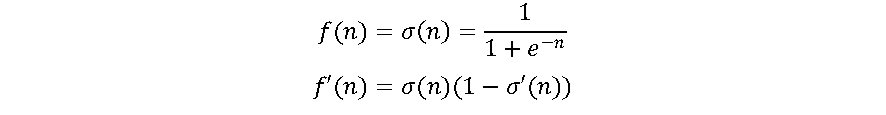
A função varia de 0 a 1 tendo um formato S. A função sigmoide essencialmente tenta empurrar os valores de Y para os extremos. Esta é uma qualidade muito desejável quando se deseja classificar os valores para uma classe específica. A função sigmoide é amplamente utilizada. Entretanto, quando os gradientes se tornam muito pequenos, a função se aproxima de zero, dificultando o aprendizado do neurônio. Sua derivada tende a 0 para valores de entrada maiores que +5 e abaixo de -5. Pelos valores de saída estarem limitados a (0,1), pode exigir algum tipo de normalização dos sinais de entrada para que sejam sempre positivos. Além disso, em geral, uma RNA composta por sigmoide utiliza mais ciclos de aprendizado do que RNAs com funções de ativação mais “rápidas” [1],[4].
2.4. Função Tangente Hiperbólica (tanh)
A tanh é outra função do tipo sigmoide. Na verdade, é apenas uma versão escalonada da função sigmóide., variando entre -1 e +1, cuja expressão e derivada são dadas pelas equações a seguir:
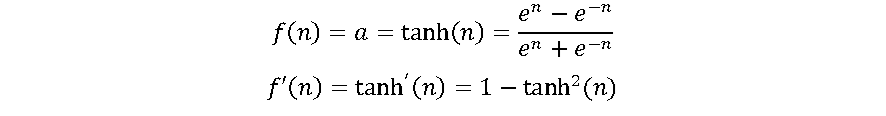
A tanh funciona de forma semelhante à função sigmóide, mas é simétrica em relação à origem, variando entre (-1,1). Ela Basicamente, soluciona o problema dos valores, sendo todos do mesmo sinal. Todas as outras propriedades são as mesmas da função sigmoide. É contínua e diferenciável em todos os pontos. A função não é linear, resultando em algoritmos de treinamento ligeiramente mais rápidos que a log-sigmoide [1],[4].
2.5. Funções Baseadas em Retificadores
A função ReLU é a unidade linear retificada (retified linear unit – ReLU). A função ReLU é muito parecida com a função identidade, fazendo com o processo de aprendizagem da RNA, baseado nessa função de ativação, seja muito mais rápido que por sigmoides [7].
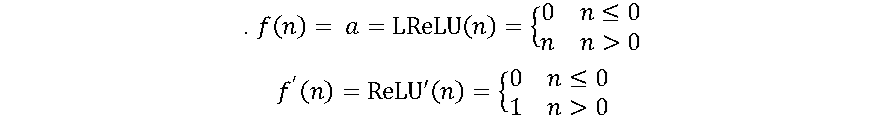
A ReLU é uma das funções de ativação mais utilizadas atualmente. A principal vantagem de usar a função ReLU é que ela não ativa todos os neurônios ao mesmo tempo. Na função ReLU, se a entrada for negativa, ela será convertida em zero e o neurônio não será ativado. Isso significa que, ao mesmo tempo, apenas alguns neurônios são ativados, tornando a rede esparsa, eficiente e de computação fácil. Essa vantagem também pode ser considerada uma desvantagem, pois os neurônios utilizando ReLU tendem a “morrer” durante o treinamento, causando a saída do neurônio iniciar a produzir apenas zeros. Uma variação da ReLU, chamada Leaky-ReLU (LReLU) evita isso [7] cuja função e sua derivada são apresentadas pelas equações a seguir:
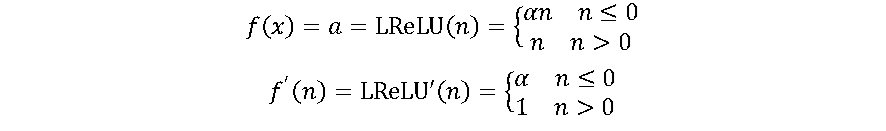
Onde α é um parâmetro introduzido na LReLU, com valores propostos entre 0.01 e 0.2 [7]. A LReLU permite o neurônio ter um pequeno gradiente quando ele não está ativo (n < 0), reduzindo o problema potencial mencionado sobre ReLU [6].
2.6. Neurônio PAL2v
O neurônio PAL2v utiliza o algoritmo da lógica paraconsistente anotada com anotação de 2 valores (paraconsistent annotated logic by 2-value annotations – PAL2v), também chamada de lógica paraconsistente anotada evidencial (paraconsistent annotated evidential logic – PAL ετ) [1]. A PAL2v é uma variação da lógica paraconsistente, proposta pelo matemático brasileiro Newton da Costa [1].
O neurônio PAL2v, quando entradas ponderadas por peso são combinadas e aplicadas à função de ativação PAL2v foi proposto em [1] e aplicado com sucesso na identificação e controle de sistemas dinâmicos não lineares [8],[9]. Ao contrário das funções de ativação que possuem uma entrada (n) e uma saída (a), o neurônio PAL2v possui 2 entradas ortogonais entre si (μ,λ). Esta característica dá uma flexibilidade muito grande ao neurônio PAL2v. Os sinais de interesse podem ser aplicados apenas a uma entrada enquanto que a outra funciona como um “bias” na função de ativação. Ou uma das entradas pode receber os sinais de interesse com pesos enquanto que a outra entrada funciona como realimentação da saída, para análise de séries temporais, como em redes neurais recorrentes (recurrent neural networks – RNN) [1],[9]. A Figura 6 apresenta um diagrama conceitual da função de ativação PAL2v.
Por ser baseada em uma lógica, os valores de μ e λ são limitados entre (0,1), por isso na figura aparece uma saturação entre esses dois valores, antes da operação da função PAL2v.
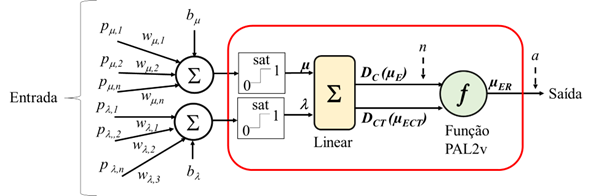
Fonte: Adaptado de [1].
A função PAL2v de forma simplificada pode ser calculada conforme a seguir:
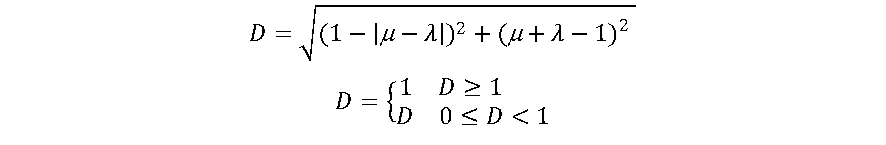
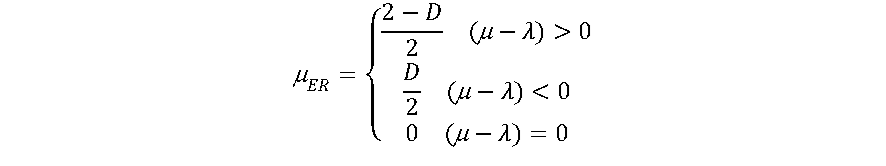
Interessante que a função de ativação PAL2v apresenta um comportamento dual. Se uma das entradas for mantida em 0.5, a saída será uma sigmoide. Do contrário a saída poderá saturar em 0.5, apresentando uma curva tipo retificadora não linear. A figura 7 apresenta a saída da função de ativação PAL2v, variando-se μ e mantendo-se λ constante Já a Figura 8 apresenta a saída da função de ativação PAL2v mantendo-se μ constante e variando-se λ [8],[9].
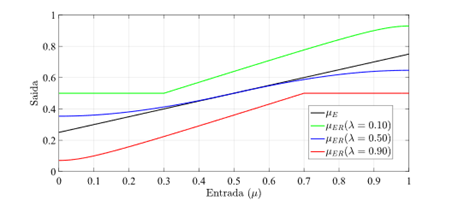
Fonte: Adaptado de [1].
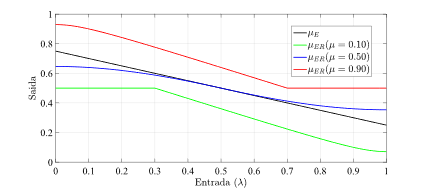
Fonte: Adaptado de [1].
O neurônio PAL2v apresentou melhor erro médio quadrático (mean square error – MSE) e menos ciclos de treinamento que RNAs equivalentes com funções sigmoide, tangente hiperbólica e LReLU para aplicações de identificação e controle de pêndulo invertido rotativo [8],[9], tanto com RNA convencional do tipo feed-forward, como em RNN [8],[9].
Uma comparação entre redes neurais utilizando as funções de ativação sigmoide, tanh, ReLU, LReLU e PAL2v em Matlab está disponível em [10].
2.7. Outras Funções de Ativação
Como dito anteriormente, existem muitas outras funções de ativação. Uma classe especial são as funções base radial (radial basis functions – RBF). Nessa categoria há uma grande quantidade de funções, tais como:
a. Gaussiana
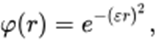
b. Multiquadrática
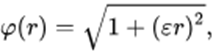
c. Inversa da Multiquadrática
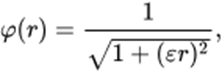
As RBFs são aproximadores universais muito extremamente eficientes. O treinamento de rede neural RBF (RBF neural network – RBFNN) é mais rápido que funções de ativação do tipo sigmoide. A desvantagem da RBFNN está na sua complexidade, que aumenta conforme o crescimento de neurônios na camada oculta. Outro desafio da RBF está em sua estrutura algoritmo de treinamento, não permitindo modela um sistema fortemente não linear [9]. Na literatura há uma grande variedade de RBFs propostas [11].
3. COMENTÁRIOS FINAIS
Este artigo procurou apresentar de forma suscinta os tipos de funções de ativação mais comuns utilizados em projetos de RNAs e suas características básicas, além de propostas que tem recebido atenção dos pesquisadores, como a função PAL2v e as RBFs.
A escolha da função de ativação da RNA passa por diversas questões tais como a complexidade da função, os algoritmos de aprendizagem da RNA, se o sistema resultará em “neurônios mortos”, se o processo de aprendizagem é suave ou apresenta dissipação do gradiente (Vanishing Gradient), qual o poder computacional exigido para o treinamento da RNA, quantos neurônios e quantas camadas são necessários, entre outros fatores.
4. REFERÊNCIAS
[1] DE CARVALHO JUNIOR, A. Identificação e Controle de Sistemas Dinâmicos com Rede Neural Paraconsistente. 2021. 196 p. Tese (Doutorado) – Programa de Engenharia Elétrica, Escola Politécnica, Universidade de São Paulo, São Paulo, 2021. Disponível em https://www.teses.usp.br/teses/disponiveis/3/3142/tde-08102021-100149/pt-br.php. Acessado em fevereiro 27, 2024.
[2] TAFNER, M. A. O que são as Redes Neurais Artificiais, Revista Cerebro e Mente 2(5), 1998. Disponível em https://cerebromente.org.br/n05/tecnologia/rna_i.htm, acessado em fevereiro 27, 2024.
[3] HAGAN, M. T.; DEMUTH, H. B.; BEALE, M. H.. Neural Network Design, Martin Hagan; 2º edition, 2014, 802 p. Disponível em https://hagan.okstate.edu/NNDesign.pdf, acessado em fevereiro 27, 2024.
[4] DSA, Função de Ativação, Deep Learning Book, Data Science Academy. Disponível em https://www.deeplearningbook.com.br/funcao-de-ativacao, acessado em fevereiro 27, 2024.
[5] SONODA, S.; MURATA, N. Neural network with unbounded activation functions is universal approximator. Applied and Computational Harmonic Analysis, Vol. 43, Issue 2, 2017, p. 233-268. DOI: 10.1016/j.acha.2015.12.005.
[6] APICELLA, A.; DONNARUMMA, F.; ISGRÒ, F.; Prevete, R. A survey on modern trainable activation functions, Neural Networks, Volume 138, p. 14-32, 2021. DOI: 10.1016/j.neunet.2021.01.026.
[7] LIU, X.; JIA, R.; LIU, Q.; ZHAO, C. AND SUN, H. Coastline Extraction Method Based on Convolutional Neural Networks—A Case Study of Jiaozhou Bay in Qingdao, China, in IEEE Access, vol. 7, p. 180281-180291, 2019. DOI: 10.1109/ACCESS.2019.2959662.
[8] A. De Carvalho, J. F. Justo, B. A. Angélico, A. M. De Oliveira and J. I. d. S. Filho, “Rotary Inverted Pendulum Identification for Control by Paraconsistent Neural Network,” in IEEE Access, doi: 10.1109/ACCESS.2021.3080176.
[9] Carvalho, A., Justo, J.F., Angélico, B.A. et al. Model reference control by recurrent neural network built with paraconsistent neurons for trajectory tracking of a rotary inverted pendulum, Applied Soft Computing, 2022, 109927, ISSN 1568-4946, DOI: 10.1016/j.asoc.2022.109927.
[10] CARVALHO, A. Paraconsistent Neural Network (PNN). MATLAB Central File Exchange. Retrieved June 13, 2023. Disponível em https://www.mathworks.com/matlabcentral/fileexchange/130739-paraconsistent-neural-network-pnn, acessado em fevereiro 27, 2024.
[11] DASH, Ch. Sanjeev Kumar; et al. Radial basis function neural networks: a topical state-of-the-art survey. Open Computer Science, vol. 6, no. 1, 2016, pp. 33-63. DOI: 10.1515/comp-2016-0005.
Elaborado Por: Dr. Arnaldo de Carvalho Junior
Publicado em: Fev 28, 2024



