PAL Eτ: A Solução para os Desafios de AIoT em Edge Computing

1. Introdução

A inteligência artificial (artificial intelligence – AI) tem se desenvolvido de forma acelerada nos últimos anos, com aplicações nas mais diversas áreas do conhecimento humano. Aprendizado de máquina (machine learning – ML), reconhecimento de fala, geração de linguagem natural, aprendizagem profunda (deep learning – DL), biometria, diagnósticos, cibersegurança, automação e robótica estão entre as principais tendências de desenvolvimento futuros em AI [1].

Outra frente de destaque de desenvolvimento tecnológico deste século é a internet das coisas (internet of things – IoT) e seus mais diversos campos de interesse, como indústrias, automação de cidades, agronegócio, logística, infraestrutura, entre outros [2].

A adição da AI ao IoT eleva este último a um novo patamar, aumentando a eficiência das operações de tecnologia da informação (information technology – IT), as interações entre homem e máquina, melhor gerenciamento e análise dos dados. A AI + IoT cria um novo paradigma tecnológico, chamado de inteligência artificial das coisas (artificial intelligence of things – AIoT) [2].

A arquitetura da IoT pressupõe uma massiva quantidade e diversidade de sensores, conectividade via rede de telecomunicações, gerando um grande volume de dados (big data) que é direcionado para processamento em nuvem ou em camada intermediária da arquitetura (fog) [2].

No entanto, há situações em que a análise, diagnóstico e tomada de decisão devem ser realizadas de forma ágil e rápida, sem atrasos. Nesses casos, o processamento ocorrendo o mais próximo da fonte de dados (sensores), o chamado processamento de borda (edge computing), é importante [2]. Infelizmente, os dispositivos de edge computing e sistemas embarcados (embedded systems) podem ter recursos computacionais limitados. A implementação de algoritmos de AI, ML, e sistemas para tomada de decisões que apresentem baixa complexidade e consumam poucos recursos são desejáveis. Neste cenário, uma tecnologia que se destaca é a lógica paraconsistente anotada evidencial (paraconsistent annotated evidential logic – PAL Eτ) [3].

A PAL Eτ pertence à família de lógicas paraconsistentes, podendo lidar com informações inconsistentes e contraditórias, sem que o peso dos conflitos invalide as conclusões. A PAL Eτ possui algoritmo robusto, matemática de baixa complexidade, reversibilidade, poucas regras e decisões. Por estas características ela vem ganhando atração entre pesquisadores das mais diversas áreas, de automação e robótica a sistemas de diagnóstico médico e tomada de decisão [3].

2. Um pouco sobre PAL Eτ

A PAL Eτ  utiliza 1 ou mais variáveis, geralmente um par (μ₁,μ₂), como anotações ou evidências em um diagrama de Lattice de 4 vértices, expressam o conhecimento sobre uma determinada proposição P. O poder de representar evidências e analisar contradições no diagrama de Lattice da PAL Eτ ficou demonstrado em uma ampla gama de pesquisas, desde partir do cálculo diferencial integral paraconsistente, ao modelo de Bohr para níveis de energia do Hidrogênio átomo, energia escura e teoria da relatividade, e até uma derivação para a lógica paraquântica [3].

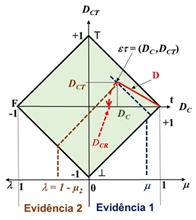
Uma das variáveis suporta a proposição P, sendo chamada de grau de evidência favorável (μ = μ₁). A outra variável será contrária à proposição P, sendo denominada de grau de evidência desfavorável (). Se ambas as variáveis suportam a proposição P, utiliza-se o complemento de uma delas como desfavorável (λ = 1 – μ₂)_. A Figura 1 a seguir apresenta o diagrama de Lattice da PAL Eτ. Uma boa descrição do algoritmo básico (Figura 2) pode ser encontrada na referência [4].

3. Aplicações da PAL Eτ  em AIoT e Edge Computing

A grande vantagem da PAL Eτ  está no uso de regras e operações matemáticas simples, o que permite criar sistemas robustos e confiáveis, mesmo em dispositivos com limitações de recursos computacionais, sendo ideal para aplicações embarcadas e de Edge Computing.

3.1 PAL Eτ ou Fuzzy?

Os computadores têm dificuldade em imitar o raciocínio humano para tomada de decisão quando o valor está entre verdadeiro e falso. Em tal situação, várias técnicas têm sido exploradas, como a lógica difusa (Fuzzy logic) [3].

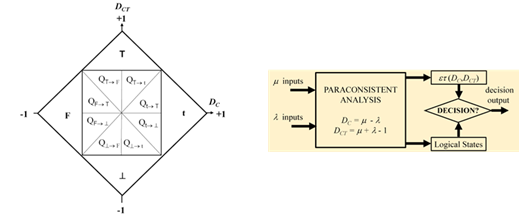
Apesar de amplamente utilizada, a lógica Fuzzy tem algumas limitações, pois pode exigir vários parâmetros, dezenas ou centenas de regras do tipo if-them, funções de associação e inferências. Além disso, o desenho de regras Fuzzy depende do conhecimento e da experiência humana. Se alta velocidade e extensas regras Fuzzy forem requeridas, pode não ser viável utilizá-la em um sistema especialista embarcado, com recursos computacionais limitados. A PAL Eτ, por outro lado, pode fornecer velocidade computacional em sistemas especialistas. Simples equações são extraídas das análises no diagrama de Lattice da PAL Eτ, facilitando o desenvolvimento de sistemas especializados com incertezas [3].

O diagrama de Lattice da PAL Eτ pode ser dividido em um certo número de regiões, ou “estados lógicos”, usados para tomada de decisões. Um exemplo típico é a divisão em 12 regiões, utilizadas, por exemplo, para a toma de decisão de direção de um robô móvel, como proposto em [5]. Um exemplo de demonstração do algoritmo da PAL Eτ em Matlab, e sua saída tanto na forma de resposta a uma proposição P, como em um de 12 estados lógicos paraconsistentes pode ser observado em [6].

3.2. PAL Eτ ou Kalman?

Em muitas situações os sensores utilizados em IoT ou em sistemas embarcados são contaminadas por ruídos e imprecisões. O filtro Kalman é um algoritmo bastante utilizado e que produz estimativas dos valores reais de grandezas medidas e valores associados predizendo um valor, estimando a incerteza do valor predito e calculando uma média ponderada entre o valor predito e o valor medido. Entre as vantagens do Filtro Kalman está o fato de ser baseado em sistemas dinâmicos lineares discretizados no domínio do tempo e operar com matrizes, permitindo a construção de sistemas de múltiplas entradas e múltiplas saídas (multiple input multiple output – MIMO). Entretanto, há situações em que um simples filtro-passa-baixas de primeira ou segunda ordem é suficiente para estimar o valor de uma variável. Para esses casos a PAL Eτ pode ser uma solução [7,8]. Conforme a Figura 4, a saída atual (μ_E[n]) do PAL2v Filter (outro nome para PAL Eτ) consiste basicamente de uma parcela (1-F_L) da saída anterior (μ_E[n-1]) mais uma parcela (F_L) da entrada atual (μ_[n]), conforme a equação apresentada na Figura 4, onde F_L corresponder ao fator de aprendizagem e é o ajuste do filtro. Pode-se cascatear várias unidades do PAL2v Filter para criar filtros de ordem superior, como demonstrado na referência [9] disponibilizada em Matlab.

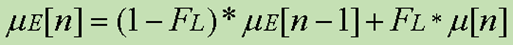
3.3. Redes Neurais Artificiais com PAL Eτ?

O algoritmo básico da PAL Eτ pode ser utilizado para compor a função de ativação de um neurônio. A interligação de vários neurônios PAL Eτ podem ser usadas para formar uma rede neural paraconsistente (paraconsistent neural network – PNN). Foi demonstrado em [10] que uma PNN apresentou vantagens em relação a redes neurais artificiais (artificial neural network – ANN) com funções de ativação clássicas (sigmoide, tanh e ReLU) para a identificação de um sistema dinâmico não linear de pêndulo invertido [10]. Da mesma forma, um sistema de controle por modelo de referência (model reference control – MRC), composto por 3 redes neurais paraconsistentes recorrentes (recurrent paraconsistent neural network – RPNN) foi implementado com sucesso no controle de um pêndulo invertido rotativo (rotary inverted pendulum – RIP), com menor esforço de energia e maior robustez que o sistema clássico de controle por alocação de polos [11]. Esse sistema utilizou apenas 14 neurônios PAL Eτ sendo executado em um microcontrolador ESP32 no controle em tempo real do RIP, demonstrando o potencial de utilização de redes neurais paraconsistentes em sistemas embarcados e de edge computing.

A Figura 5 apresenta um exemplo de PNN. Uma comparação entre PNN e ANN na forma de algoritmo de Matlab está disponível na referência [12].

4. Considerações Finais

Esse post apresentou alguns algoritmos e suas aplicações bem-sucedidas da PAL Eτ na tomada de decisões, filtragem e tratamento de sinal, classificação, reconhecimento de padrões, identificação e controle. A simplicidade das equações e regras da PAL Eτ são características importantes e que devem ser levadas em consideração em projetos de sistemas AIoT embarcados e de computação de borda.

Para saber mais sobre a PAL Eτ, um bom começo pode ser a pagina “PAL2v: Key Points”, que complementa as referências listadas neste post e está disponível em: https://sites.google.com/view/prof-arnaldo/pal2v-key-points. Acessada em 09 jan 2024. Nela há referência aos principais algoritmos, os links para exemplos em Matlab e um conjunto de artigos de referência de alto fator de impacto sobre a lógica.

Referências

[1] De Carvalho Junior, A. 10 Tendências de Aplicação de Inteligência Artificial em 2024! EAILAB, publicado em nov 28, 2023. Disponível em: https://eailab.labmax.org/2023/11/28/10-tendencias-de-aplicacao-de-inteligencia-artificial-em-2024/

[2] De Carvalho Junior, A. Tendências em Edge Computing. EAILAB, publicado em dez 12, 2023. Disponível em: https://eailab.labmax.org/2023/12/12/tendencias-em-edge-computing/

[3] De Carvalho Junior, A.; Justo, J. F.; De Oliveira, A. M.; Da Silva Filho, J. I., A comprehensive review on paraconsistent annotated evidential logic: Algorithms, Applications, and Perspectives, Engineering Applications of Artificial Intelligence, Volume 127, Part B, 2024, 107342, ISSN 0952-1976 DOI: 10.1016/j.engappai.2023.107342.

[4] Da Silva Filho, J. I. Treatment of Uncertainties with Algorithms of the Paraconsistent Annotated Logic, Journal of Intelligent Learning Systems and Applications, Vol. 4 No. 2, 2012, pp. 144-153. DOI: 10.4236/jilsa.2012.42014. Disponível em:  https://www.scirp.org/journal/paperinformation.aspx?paperid=19263. Acessado em dez 21, 2023.

[5] Abe, J.M., Torres, C.R., Lambert-Torres, G., Nakamatsu, K., Kondo, M., 2006b. Intelligent paraconsistent logic controller and autonomous mobile robot emmy II. In: Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, pp. 851–857. http://dx.doi.org/10.1007/11893004_108.

[6] De Carvalho Junior, A. (2023). PAL2v Para-Analyzer, MATLAB Central File Exchange. Retrieved November 22, 2023. Disponível em: https://www.mathworks.com/matlabcentral/fileexchange/155422-pal2v-para-analyzer. Acessado em dez 21, 2023.

[7] De Carvalho Jr., A. et al. (2023). A Paraconsistent Artificial Neural Cell of Learning by Contradiction Extraction (PANCLCTX) with Application Examples. In: Abe, J.M. (eds) Advances in Applied Logics. Intelligent Systems Reference Library, vol 243. Springer, Cham. DOI: 10.1007/978-3-031-35759-6_5.

[8] Carvalho, A., Justo, J.F., Angélico, B.A. et al. Paraconsistent State Estimator for a Furuta Pendulum Control. SN COMPUT. SCI. 4, 29 (2023). https://doi.org/10.1007/s42979-022-01427-z

[9] De Carvalho Junior, A. (2023). PAL2v Filter, MATLAB Central File Exchange. Retrieved May 24, 2023. Disponível em: https://www.mathworks.com/matlabcentral/fileexchange/129644-pal2v-filter. Acessado em dez 21, 2023.

[10] Carvalho, A., Justo, J. F., Angélico, B. A. et al, “Rotary Inverted Pendulum Identification for Control by Paraconsistent Neural Network,” in IEEE Access, doi: 10.1109/ACCESS.2021.3080176.

[11] Carvalho, A., Justo, J.F., Angélico, B.A. et al. Model reference control by recurrent neural network built with paraconsistent neurons for trajectory tracking of a rotary inverted pendulum, Applied Soft Computing, 2022, 109927, ISSN 1568-4946, DOI: 10.1016/j.asoc.2022.109927.

[12] De Carvalho Junior, A. Paraconsistent Neural Network (PNN), MathWorks, Retrieved June 13, 2023.  Disponível em: https://www.mathworks.com/matlabcentral/fileexchange/130739-paraconsistent-neural-network-pnn. Acessado em Dez 21, 2023.

Elaborado Por: Dr. Arnaldo de Carvalho Junior

Publicado em: Jan 09, 2024